How to calculate angular size

The angular diameter can alternatively be . In astronomy, the sizes of objects in the sky are often given in terms of their angular diameter as seen from Earth, rather than their actual sizes. You can convert length units here. The unit of the angle is degrees or radiant.

For objects with small angular sizes , such as typical astronomical objects, the precise relationship between angular size , actual size and distance is well approximated by the equation : angular size = (actual size ÷ distance).

In this article, we look at how we calculate them and why they are useful.

This phenomenon is known as the angular diameter.

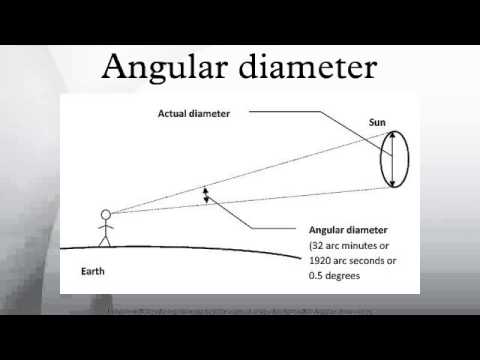
How to use observed angles and distances to work out sizes and distances. ISS measured meters across, what was its angular size in arcseconds? This demo shows how to calculate the size of the Moon and the Sun, given angular size and distance. It derives the equations necessary. For instance, the angular diameter of the full moon is about half . Problem - The distance to the cluster is 25light years.

What is: A) the smallest star separation and B) the diameter of the x- ray cluster? Astronomers measure the sizes of objects in the sky in terms of their angular size. Therefore, the only thing we can measure when we look at the sky are angular sizes and angular distances.

Jupiter = 94000km 202= is required (arcseconds per radian). When the distance is the same, the angular size is proportional to the diameter. If you draw lines from your eye to two edges of the Moon, the angle between the lines is the angular size of the Moon. In astronomy, all of the objects you see in the sky can only be compared by their angular size as measured from where you are standing.

Size and Distance of an Object . Without knowing their distances,. The corresponding sides of similar triangles are proportional to one another as the illustration to the left shows. Because the vertex angle of the triangles are identical in measure , two objects at different distances from the vertex will subtend the same angle, a. In astronomy, we often use angular measurements to describe the apparent size of an object in space and the apparent distances between objects.

Often these angles are very small. Calculate the linear size from the angular size or diameter and the distance between the object and the observer. A guide on how to use your hands and fingers to measure the sky and the distances between stars and other celestial objects.

It can also help locate specific objects in the. A simple yet fundamental concept in astronomy is angular measure. To illustrate this error, try describing the size of the Sun from your point of view. This is the fundamental formula for determining angular scales in astronomy and remote sensing. These distances are measured in degrees and radians.

If the diameter of the moon is. Problem - The relationship between angular size , Θ, and actual size, L, and distance . Angular Measure : Degrees, Minutes, and Seconds of Arc. The apparent sizes of distant objects and things in the sky are measured by the angle they subtend at the eye. Angular size has two measurements, the angular distance and the angular diameter.

Taking measurements of the angular size of the moon is also determining the angular distance of the two objects. One basic example of using the angular distance is the angle between your arms. Each fingers from both sides of the arms .